1. Алгебра
  2. Объясните , как решать:

Объясните , как решать: в каких точках касательная к графику функции f(x) = х³ /3 - 5х²/2 + 7х - 4 образует с осью ох угол 45 градусов?

8AnnaMur8 8AnnaMur8    2   12.06.2019 19:30    0

Ответы
филькатв филькатв  10.07.2020 07:18
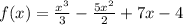
f(x)= \frac{x^{3}}{3}-\frac{5x^{2}}{2}+7x-4
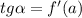tg \alpha =f'(a) - тангенс угла наклона касательной равен значению производной в точке касания a
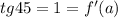tg45=1=f'(a) - тангенс 45 градусов равен 1, значит производная в точке касания а тоже должна быть равной 1.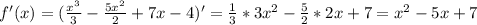
f'(x)= (\frac{x^{3}}{3}-\frac{5x^{2}}{2}+7x-4)'=\frac{1}{3}*3x^{2}-\frac{5}{2}*2x+7=x^{2}-5x+7
f'(a)=a^{2}-5a+7=1
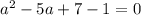
a^{2}-5a+7-1=0
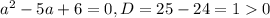
a^{2}-5a+6=0, D=25-24=10
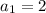a_{1}=2  - ответ
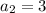a_{2}=3  - ответ
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
sek071001p0ancj sek071001p0ancj  24.11.2020 07:22
прикрепленный файл,1 задача 7 класс...
evalissa17 evalissa17  24.11.2020 07:12
Упростите выражение. 11 класс. Алгебра...
Аннабель0Свит Аннабель0Свит  19.04.2021 09:13
найти стационарные и критические точки !! f(x) = 8+4/x...
kayumovtanvir89 kayumovtanvir89  19.04.2021 09:14
нужно сделать максимально оперативно [задание границы] Умоляю вас . Заранее ( )​...
misik1 misik1  19.04.2021 09:14
Знайти суму нескінченної геометричної прогресії 80,30,11,25..​...
plenkinanatash plenkinanatash  19.04.2021 09:15
Определите не менее 3-х доказательств, остановивших междоусобную войну между султанами при правлении Жангир хана. ​...
Evgenchee Evgenchee  19.04.2021 09:15
Розв’яжіть рівняння за формулою: а)3х2-8х-3=0; б)4х(х-2)+х2=6х+3...
никак45 никак45  17.04.2020 11:44
Рaзложите на множители квадратный трехчлен 7x+x^2+12 решение нужно и ответ​...
Polly2011 Polly2011  17.04.2020 11:44
1. Укажите отрезок который является перпендикуляром проведённым из точки A к прямой BD 2. Объясните какой отрезок называется наклонной проведённой из данной прямой....
danadv danadv  17.04.2020 11:45
Реши методом алгебраического сложения систему уравнений. {8y−7x=−9 {8y+x=2 ответ: (при необходимости ответ округли до десятитысячных!) x= y=...

Популярные вопросы