нужно решить с системы нелинейных уравнений. У брата было x͟ груш, а у сестры — y͟ яблок. Всего у них было 11 этих фруктов. Если бы у брата было y͟ груш, а у сестры – x͟- яблок, то всего этих фруктов у них было бы 7. Сколько было
груш у брата и сколько яблок у сестры?
Другие вопросы по теме Алгебра
Популярные вопросы
- Решите неравенства: х^2-3х 0 х^2-7х-30 0...
1 - Как правильно поставить слова все на свои места(чтобы получилось...
1 - С. поставьте род имен существительных. : трансформатор, инкубатор,...
2 - Рисунке 111 расскажите об особенностях высотной поясности в...
3 - Риби: наявність грудної клітини амфібії: наявність грудної клітини...
2 - Периметрі 48см квадраттан диаметрі сол квадраттың қабырғасының...
1 - Синтаксический разбор предложения зовут его василий васильевич...
1 - Кто стал первым госудурем всея руси...
1 - Іть написати есе що робить мене щасливим дуже ...
3 - 1) |х+3| 7 2) |5-х|≤9 3) |11+х|≥11 4) |1,5-х| 8 5) |х+9,3|≤10,3...
3
Правильное условие такое:
У брата х груш, а у сестры у² яблок. Вместе у них было 11 этих фруктов. Если бы у брата было у груш, а у сестры -х² яблок, то всего этих фруктов у них было бы 7. Сколько было груш и сколько было яблок?
Решение.
ОДЗ:

Методом подбора быстрее.
1) Начнем с решения второго уравнения.
Если то 7-1=6. Тогда
то 7-1=6. Тогда  не натуральное число.
не натуральное число.
Если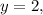 то 7-2=5. Тогда
то 7-2=5. Тогда 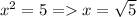 не натуральное число.
не натуральное число.
Если то 7-3=4. Тогда
то 7-3=4. Тогда 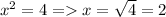 натуральное число.
натуральное число.
Получили решение
2) Подставим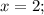
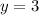 в первое уравнение
в первое уравнение  .
.
ответ: 2 груши у брата;
3 яблока у сестры.