Нужно решить, кто не будь напишите уравнение касательной к графику функции у=f(x) в точке (а; f(а) б) f(x)=1/2 под корнем х+1, а=4 в)f(x)=3-x^2+x4, а=-1 напишите уравнение касательной к графику функции у=f(x), проведенной через точку с абсциссой х0=1 б)у=3-х/х-2 г)у=х-4 под корнем х движение задано формулой s(t)=0,24t^3+2t^2-3. найдите ред днюю скорость движения в промежутке от t=4 до t=8 и мгновенную скорость в промежутке от t=4 до t=8.
Другие вопросы по теме Алгебра
Популярные вопросы
- В1 кг сахара содержится 150 г жира. каков процент жироности сливок?...
2 - Какие особенности грибов в жизни человека?...
3 - Сенбернари – одна із найбільших порід собак. висота їх досягає 80-95 сантиметрів....
2 - Периметр квадрата равен периметру прямоугольника площадью 100 см 2 , а его ширина...
3 - Два парохода вышли одновременно из двух портов навстречу другу другу.скорость первого...
3 - 287+562+432*2/5 запишите ответ, не по действиям...
3 - Почему для загара используются специальные защитные средства? 1.чтобы кожа была...
2 - Какое произведение из других разделов учебника ты включил бы в раздел животные в...
2 - 1) какие взаимоотношения в обществе регулируют гражданские правоотношения 2)тенденции...
2 - Как написать предложение со словом проверить исправность...
2
Скоростью является первая производная пути т.е.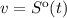 , тогда ⇒
, тогда ⇒
ответ: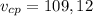 м/с.
м/с.