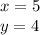нужно решить эти две систему уравнений с дискриминанта 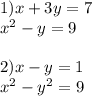
Другие вопросы по теме Алгебра
Популярные вопросы
- Шахматный конь гулял по клеткам фигуры, изображенной на первом рисунке....
3 - У меня компа нету, если что дам почту свою...
1 - Знайдіть сторону ромба якщо його периметр дорівнюе 36 см...
2 - 2-тапсырма Тындалған мәтін бойынша жалпы және нақты сұрақтарға жауап бер....
3 - 1)виды соединительных швов.? 2) Как ещё называют соединительные швы?3)...
2 - Значение пяти выражений соли равно 5. 6. 7. 8. 9. В каждом из них используйте...
2 - Начертите проекцию: Вид сверху Вид сбоку Вид спереди (главный вид)...
1 - Составить план пути Абая домой...
3 - Можно 10-е задание очень нужно...
1 - решить задачу Катер массой m = 1,5 т начинает движение по озеру под действием...
1
1)
ОТВЕТ: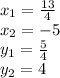
2)
ОТВЕТ: