1. Алгебра
  2. Нужно найти нули функции y=x^3-5x^2-4x+20

Нужно найти нули функции y=x^3-5x^2-4x+20

fukurochanmiup04xjx fukurochanmiup04xjx    3   03.10.2019 18:40    0

Ответы
еккаа еккаа  09.10.2020 15:06

y=x^3-5x^2-4x+20

Нули функции будут находиться среди делителей числа 20. Проверим х=2: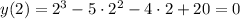  y(2)=2^3-5\cdot 2^2-4\cdot 2+20=0 .  Значит х=2 - корень многочлена. Теперь разделим многочлен на разность (х-2), тогда

\frac{x^3-5x^2-4x+20}{x-2}=x^2-3x-10\\\\x^3-5x^2-4x+20=(x-2)(x^2-3x-10)\\\\x^2-3x-10=0\; \; \Rightarrow \; \; x_1=-2\; ,\; x_2=5\; \; (teorema\; Vieta)\; \; \Rightarrow \\\\x^2-3x-10=(x-2)(x+5)\\\\x^3-5x^2-4x+20=(x-2)(x-5)(x+2)\\\\Otvet:\; \; x_1=2\; ,\; x_2=5\; ,\; x_3=-2\; .

ПОКАЗАТЬ ОТВЕТЫ
SofiLand854 SofiLand854  09.10.2020 15:06

Один корень легко подобрать или угадать это х=2.

Потом делим правую часть на х-2 и получаем квадратное уравнение

х^2-3х-10=0

Решаем его по теореме Виета и находим еще 2 корня

х=5 и х=-2.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
alina067 alina067  06.12.2020 03:24
У меня уже дипрессия Номера 211, 213 учительница меня убьёт. напишите на листочке а то я ничего не пойму​...
НЕЗНАЙКА2283371 НЕЗНАЙКА2283371  31.10.2020 12:48
Найдите коэффициент при x ^ n в классификации бинома 1) (х +2)^10, n= 3; 2) (1 - 2x)^7, n=4; 3) (√x - 2/x)^8, n= -5: Помагите заранее...
Чеширский1 Чеширский1  31.10.2020 12:48
5. Теңдеуді шешіңіз және жа424 : (3х – 17) = 4​...
Adn2001 Adn2001  31.10.2020 12:49
Найдите коэффициент при x ^ n в классификации бинома 1) (х +2)^10, n= 3; 2) (1 - 2x)^7, n=4; 3) (√x - 2/x)^8, n= -5: Помагите заранее...
karandash72772 karandash72772  25.12.2019 14:57
Найдите производную функции y=5x^-4 -1\x3 - 2кореньиз x + 2корень из 3x - кореньиз 5 ( нужно) заранее...
Мухлисуллин Мухлисуллин  25.12.2019 15:02
Решитеесли не сложно то побыстрее​...
joraninga joraninga  25.12.2019 15:03
Разложить на множители -3/7x^2-6/7xy-3/7y^2​...
amaykovska amaykovska  25.12.2019 15:03
Является ли число -36 членом арифметической прогрессии 32, 31, 2, с 1является . то указките его номер.​...
мархабабурсакова6565 мархабабурсакова6565  25.12.2019 15:03
Монету подбрасывается 12 раз.а)сколько получится различных последовательностей состоящих из орлов и решек б)сколько получится различных последовательностей из 8 орлов и 6 решек с)какова...
Сонякака332 Сонякака332  25.12.2019 15:04
1.развязать систему неравенства 2.развязать двойное неравенство 3.при каких значениях переменная имеет смысл выражения...

Популярные вопросы