Нужно исследовать функции на четность (четная/нечетная) а) y=-x^4+8x^2 б) y=x^2-1/x
Другие вопросы по теме Алгебра
Популярные вопросы
- Твір роздум на тему: бійтеся своїх думок : вони-початок ваших вчинків...
1 - Предположите , почему представители разных сословий по-разному относились к возможной...
1 - Катализатор, применяющийся в процессе крекинга? плз...
1 - Биология 7 сопоставьте правильно....
2 - Найдите значение выражения (а^2-a^7+a^3): (-a^2)+(a+1)^2 если а=-1 40...
2 - Из-за чего детей ставят на учет в полицию что нужно что б сняли с учета в интернете...
3 - Составьте выражение из суммы чисел 13 479 и 16 397 знака деления и разности чисел...
1 - Будет ли словочетание если только будет предлог...
3 - Сколько орфограмм можно выделить в предложении: бежит в зеленой чаще веселый ключ...
3 - Напишите доклад по обж на тему: что делать если я встретил гадюку...
3
если функция четная, то , если нечётная, то
, если нечётная, то 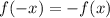 , если не подходит ни туда, ни сюда, то она не является ни четной, ни нечетной
, если не подходит ни туда, ни сюда, то она не является ни четной, ни нечетной
а)1)Область определения - симметричное множество, x-любое ( погугли, что это такое)
2)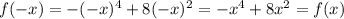
Из п. 1 и 2 мы делаем вывод, что функция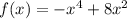 - четная функция
- четная функция
б)1)Область определения - симметричное множество,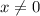
2)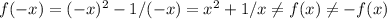
Из п. 2 мы делаем вывод, что функция не является ни четной, ни нечетной.