Номер 1.найдите площадь треугольника,образованного осями координат и касательной к графику функции: y =х\2х-1 в точке х=-1 номер 2.докажите,что функция y=корень из 2 х удовлетворяющее соотношению 1\y3 + y"=0 номер 3.
напишите уравнение касательной к графику функции: y= sinквадратх в точке х=минус п\4 надо,

Ответы

lubvic77 24.05.2020 04:47

1. Только что решала вот тут

2. Не совсем понятно условие... Соотношение такое: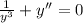 $\frac{1}{y^3}+y''=0$ ?

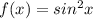
3. f(x) = sin^2x

$x_0 = -\frac{\pi}{4}$

y = f(x0) + f'(x0)(x-x0) - общий вид уравнения касательной к графику функции f(x) в точке x0.

f'(x) = 2sinx*cosx = sin2x

$f(x_0) = sin^2(-\frac{\pi}{4}) = \frac{1}{2}$

$f'(x_0) = sin(-2\frac{\pi}{4}) = -sin\frac{\pi}{2} = -1$

$y = \frac{1}{2}-1(x+\frac{\pi}{4})$ - уравнение касательной

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра

kurokislip 31.05.2019 17:50

tor142003 31.05.2019 17:50

Найдите сумму первых пяти членов прогрессии b3=-18 q=3...

erkin0268 31.05.2019 17:50

1)sin4a/1-cos4a 2)cos2a*sin2a/2tg2a...

Vladislava256 12.11.2020 09:03

решить. Выполните действия с рациональными дробями...

miragrrr 12.11.2020 09:03

pikuss 12.11.2020 09:04

1. у=7х3-9х^2+15 2. у=11+4х 3. у= 4. у=log3x...

zannaeroshik505 12.11.2020 09:05

lollllla1 12.11.2020 09:05

(6x-4)*(5-x)=0 решите нужно...

сархан2007 12.11.2020 09:05

Lev1111111111 12.11.2020 09:05