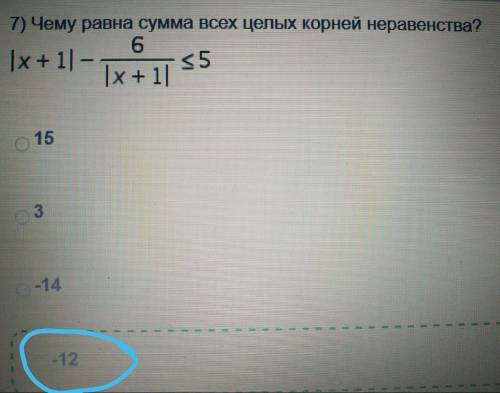
Неравенство с модулем нужно объяснение правильный ответ отмечен)

Ответы

Пелагея9087 15.10.2020 13:30

-12

Объяснение:

Всё читай на фото................. Было интересно за вопрос.

ПОКАЗАТЬ ОТВЕТЫ

lybabibrka 15.10.2020 13:30

$|x+1|-\frac{6}{|x+1|} \leq 5$

Пусть |x+1| = t, t > 0 (т.к. на ноль делить нельзя), тогда

$t-\frac{6}{t} \leq 5$ | * t

t²- 6 - 5t ≤ 0

t² - 5t - 6 = 0

D = (-5)² - 4 * (-6) = 25 + 24 = 49 = 7²

$t_{1} = \frac{5+7}{2*1} = \frac{12}{2} = 6$

$t_{2} = \frac{5-7}{2*1} = - \frac{2}{2} = -1$

t∈[-1 ; 6] , но т.к. t > 0 ⇒ t∈( 0 ; 6 ]

Вернёмся к замене

Т.к. нам нужны целочисленные решения, то получаются следующие решения :

$\left[\begin{array}{ccc}|x+1| = 1\\|x+1| = 2\\|x+1| = 3\\|x+1| = 4\\|x+1| = 5\\|x+1| = 6\end{array}$

Раскрываем модули:

$\left[\begin{array}{ccc}\left \{ {{x+1=1} \atop {x+1=-1}} \right. \\\left \{ {{x+1=2} \atop {x+1=-2}} \right.\\\left \{ {{x+1=3} \atop {x+1=-3}} \right.\\\left \{ {{x+1=4} \atop {x+1=-4}} \right.\\\left \{ {{x+1=5} \atop {x+1=-5}} \right.\\\left \{ {{x+1=6} \atop {x+1=-6}} \right.\end{array}$

Решим каждую систему по отдельности

$\left \{ {{x+1=1} \atop {x+1=-1}} \right. = \left \{ {{x=1-1} \atop {x=-1-1}} \right. = \left \{ {{x=0} \atop {x=-2}} \right.$

$\left \{ {{x+1=2} \atop {x+1=-2}} \right. = \left \{ {{x=2-1} \atop {x=-2-1}} \right. = \left \{ {{x=1} \atop {x=-3}} \right.$

$\left \{ {{x+1=3} \atop {x+1=-3}} \right. = \left \{ {{x=3-1} \atop {x=-3-1}} \right. = \left \{ {{x=2} \atop {x=-4}} \right.$

$\left \{ {{x+1=4} \atop {x+1=-4}} \right. = \left \{ {{x=4-1} \atop {x=-4-1}} \right. = \left \{ {{x=3} \atop {x=-5}} \right.$

$\left \{ {{x+1=5} \atop {x+1=-5}} \right. = \left \{ {{x=5-1} \atop {x=-5-1}} \right. = \left \{ {{x=4} \atop {x=-6}} \right.$

$\left \{ {{x+1=6} \atop {x+1=-6}} \right. = \left \{ {{x=6-1} \atop {x=-6-1}} \right. = \left \{ {{x=5} \atop {x=-7}} \right.$

Получается

$\left[\begin{array}{ccc}\left \{ {{x=0} \atop {x=-2}} \right. \\\left \{ {{x=1} \atop {x=-3}} \right.\\\left \{ {{x=2} \atop {x=-4}} \right.\\\left \{ {{x=3} \atop {x=-5}} \right.\\\left \{ {{x=4} \atop {x=-6}} \right.\\\left \{ {{x=5} \atop {x=-7}} \right.\end{array}$