Неравенство (х-а)(2х-1)(х+b)>0 имеет решение (-8;1)∪(10;+∞).Найдите значение а и b.
Другие вопросы по теме Алгебра
Популярные вопросы
- Допишите последние фразы приводя убедительные аргументы (в стиле диалога). обратите...
1 - Вероника в спортивном магазине купила мяч, набор для бадминтона и скакалку. на покупку...
3 - Кэтому тексту 3 вопроса yes/no-question,3 вопроса or-question,3 вопроса wh-question...
3 - Выполните морфологический разбор 1.кто сам собой не ,тот и другого не наставит....
1 - Ресурс аты . жаратылысы бойынша қай топқа кіреді. өндірілетін жері. қолданылуы 7...
1 - 1)8,3-(-3,2+x)=12. 2)-(2,25)+4,88=1,3 3) (x+16,35)-0,17=25,3. 4)27,8-( x+15)=17,2....
3 - Выражение и найдите его значение 1 целая 2/3 x + 2 целых 5/6x -1 целая 3/4x,если...
1 - Падрыхтуйце вуснае пра галоўнага героя апавядання- тоніка. звярніце ўвагу на тое...
3 - Запишіть речення з числівника: триста дев яносто два і триста дев яносто другий...
3 - Быстро меняющие тенденции это плохо или хорошо и что это вообще такое ...
3
Неравенство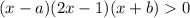 имеет решение
имеет решение
Но числа 1 не может быть на числовой оси так как нет в неравенстве скобки (х-1) .
Но есть скобка (2х-1) , откуда нуль функции должен быть при х= 1/2 .
Тогда должно было бы быть записано решение
Тогда получили бы 2 случая: