не могу понять как правильно решить систему √x + √y = 5
√ 4 степени из x + √ 4 степени из y = 3
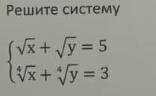
Другие вопросы по теме Алгебра
Популярные вопросы
- A24. НайдитеНайдите на каждом рисунке пару равных прямоугольных треогольников и...
3 - Сколько в среднем будет стоить 1 литр краски:188 руб.(1 л.),198 руб.(1 л.),298 руб.(1...
1 - В ідеальній тепловій машині за до кожного кілоджоуля теплоти, переданого нагрівачем,...
3 - Составить структурную формулу ввещества, построить для него 1 изомер и назвать его...
1 - Сколько миллилитров водорода (н.у.), который может быть получен при растворении...
3 - Каким должен быть наибольший диаметр пор в гнете (волокне) нагревательного устройства...
2 - Зелёные одноклеточные водоросли используются человеком в различных биотехнологических...
1 - Написати твір роздум на тему «Як написати історію» До ть будь ласка...
3 - Правильно напишіть слова і словосполучення з великої або малої літери, обґрунтуйте...
2 - Complete the interview questions with the correct words: achievement, approach,...
3
ответ: (1;16)∪(16;1)
Объяснение:
Пусть x^(1/4)=u, y^(1/4)=v, тогда √x=u²,√y=v² и система перепишется так:
u²+v²=5
u+v=3
Из второго уравнения находим v=3-u. Подставляя это выражение в первое уравнение и приводя подобные члены, приходим к квадратному уравнению u²-3*u+2=0. Оно имеет решения u1=1 и u2=2, откуда v1=3-u1=2, v2=3-u2=1. Отсюда получаем две системы уравнений:
x^(1/4)=1
y^(1/4)=2
и
x^(1/4)=2
y^(1/4)=1
Решая их, находим x1=1, y1=16, x2=16, y2=1.