Найти значение выражения 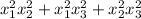, используя теорему Виета, если 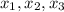корни уравнения 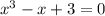можно с объяснениями, тк хочется разобраться в теме(

Question

Алгебра: Найти значение выражения , используя теорему Виета, если корни уравнения можно с объяснениями, тк хочется разобраться в теме(

КириллГромов2000 · Answer

Согласно теореме Виета для кубического уравнения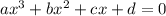 ax^3+bx^2+cx+d=0 корни этого уравнения удовлетворяют следующим условиям:

$x_1 + x_2 + x_3 = -\frac{b}{a} \\x_1x_2 + x_2x_3 + x_1x_3 = \frac{c}{a} \\x_1x_2x_3 = -\frac{d}{a}$

В заданном уравнении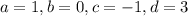 a=1,b=0,c=-1,d=3 , поэтому перепишем условия:

$x_1 + x_2 + x_3 = 0 \\x_1x_2 + x_2x_3 + x_1x_3 = -1 \\x_1x_2x_3 = -3$

Возведём обе части второго уравнения во вторую степень:

$(x_1x_2 + x_2x_3 + x_1x_3)^2 = 1 \\$

Для раскрытия скобок воспользуемся формулой:

(a+b+c)^2 = a^2+b^2+c^2+2(ab+bc+ac)

Таким образом:

x_1^2x_2^2 + x_2^2x_3^2 + x_1^2x_3^2 + 2(x_1x_2x_2x_3+x_2x_3x_1x_3+x_1x_2x_1x_3) = 1

Из скобок вынесем общий множитель:

x_1^2x_2^2 + x_2^2x_3^2 + x_1^2x_3^2 + 2x_1x_2x_3(x_2+x_3+x_1) = 1

Первые три слагаемых образуют искомое выражение, а все остальные части этого выражения можем заменить на числа (смотрим на условия, описанные в начале решения):

$x_1^2x_2^2 + x_2^2x_3^2 + x_1^2x_3^2 + 2\cdot (-3)\cdot 0 = 1\\x_1^2x_2^2 + x_2^2x_3^2 + x_1^2x_3^2=1$

ответ: 1

Найти значение выражения , используя теорему Виета, если корни уравнения можно с объяснениями, тк хочется разобраться в теме(

Популярные вопросы