Найти значение выражения 2cosa*cosb если a-b=пи/2, а синус 2b = 0,8

Question

Алгебра: Найти значение выражения 2cosa*cosb если a-b=пи/2, а синус 2b = 0,8

valia01022004 · Answer

1) Из ОТТ найдем cos2b(ОТТ-основное тригонометрическое тождество)

cos2b=0,6

2) по формуле косинуса двойного угла cos2b=2(cosb)^2-1

от сюда (cosb)^2=0,8 => cosb=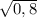 $\sqrt{0,8}$

3)Из ОТТ найдём sinb

sinb=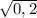 $\sqrt{0,2}$

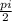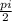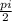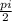4)т.к. a=b+ $\frac{pi}{2}$ , то cosa=cos(b+ $\frac{pi}{2}$ )=cosb*cos( $\frac{pi}{2}$ )-sinb*sin( $\frac{pi}{2}$ )

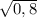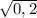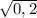
cosa= $\sqrt{0,8}$ *0- $\sqrt{0,2}$ *1=- $\sqrt{0,2}$

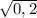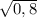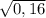5) 2cosa*cosb=-2* $\sqrt{0,2}$ * $\sqrt{0,8}$ =-2* $\sqrt{0,16}$ =-2*0,4=-0,8