Найти все корни, принадлежащие отрезку [-2П;-П/2]
x=-П/3+2пк, x=4П/3+2пк, x=П/2+пк
Должны получится такие корни: -3п/2, -п/2, -2п/3
Мне нужен сам процесс нахождения этих корней

Ответы

KapitanNEMO 03.08.2020 19:50

просто подряд подставлять целые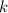

при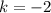 k=-2 имеем корни

$x_1=-\frac{\pi}{3}-4\pi=\frac{-13\pi}{3},\\x_2=\frac{4\pi}{3}-4\pi=-\frac{8\pi}{3},\\x_3=\frac{\pi}{2}-2\pi=-\frac{3\pi}{2}$

Первые два в промежуток не попадают, третий - попадает.

при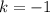 k=-1 имеем корни

$x_1=-\frac{\pi}{3}-2\pi=-\frac{7\pi}{3},\\x_2=\frac{4\pi}{3}-2\pi=-\frac{2\pi}{3}\\x_3=\frac{\pi}{2}-\pi=-\frac{\pi}{2}$ ,

первый корень в промежуток не попадает, другие два - попадают.

Если подставлять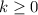 $k\geq 0$ , то увидим, что полученные в итоге корни уже не будут вписываться в границы отрезка.

универсальный, но не очень удобный): оценить и проверить, при каких целых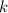 неравенство 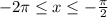$-2\pi\leq x\leq -\frac{\pi}{2}$ имеет решение. Для этого все серии корней по отдельности подставляем вместо :

$1) -2\pi\leq -\frac{\pi}{3}+2\pi k\leq -\frac{\pi}{2} |\cdot\frac{3}{\pi} ,\\-6\leq -1+6k \leq -\frac{3}{2}|+1\\-5\leq 6k\leq -\frac{1}{2} |:6\\-\frac{5}{6}\leq k\leq -\frac{1}{12}.$

Очевидно, что целых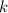 , удовлетворяющих последнему неравенству, не существует. Т.е. ни один из корней этой серии промежутку не принадлежит.

$2) -2\pi\leq \frac{4\pi}{3}+2\pi k \leq -\frac{\pi}{2}|\cdot\frac{3}{4\pi}\\ -\frac{3}{2} \leq 1+\frac{3}{2}k\leq -\frac{3}{8}|-1\\-\frac{5}{2}\leq \frac{3}{2}k\leq -\frac{11}{8}|\cdot\frac{2}{3}\\-\frac{5}{3}\leq k\leq -\frac{11}{12}$

Последнему неравенству удовлетворяет только одно целое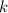 - 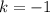k=-1 . Корень находим при подстановке значения 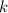в соответствующую серию.

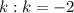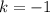То же можно проделать с третьей серией и убедиться, что неравенство удовлетворяют только 2 значения k: k=-2 и k=-1 . Их также подставляем в соответствующую серию и находим корни.