Найти все целые значения k, при которых уравнение coskx= 1+2cos^2((x/2)+(pi/4)) имеет решение. Найти эти решения.
Другие вопросы по теме Алгебра
Популярные вопросы
- Горе от ума. почему эти люди важны для тайного общества репетилова?...
2 - Найдите радиус окружности, вписанной в прямоугольный треугольник, если радиус...
1 - Выпишите из бородино (стих) восклицательные и невосклицательные предложения...
3 - Вакваріум довжиною 30 см і шириною 20 см налили води 25 см. який об єм акваріума?...
3 - Координаты точки пересечения прямых...
3 - Нужно составить 3-4 предложения про хобби на , мне нужно написать про катание...
2 - Реки на картах чаще всего изображаются с...
3 - Написать сочинение на тему капитанская дочка белогорская крепость в жизни...
1 - Составте верные равенства и неравенства используя выражения 8+6-1; 8+(6-1)...
2 - Напишите 5 сложных предложений на любую тему...
2
1-й случай. k=0; тогда второму уравнению удовлетворяют все x (при m=0), поэтому решениями первоначального уравнения будут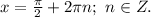
2-й случай. тогда
тогда  поэтому нужно приравнять
поэтому нужно приравнять
Каково бы ни было целое и каково бы ни было целое n, существует целое m, вычисляемое по этой формуле. Вывод: k должно делиться на 4, а решением уравнения служат
и каково бы ни было целое n, существует целое m, вычисляемое по этой формуле. Вывод: k должно делиться на 4, а решением уравнения служат 