Найти уравнение касательной для функции y =x ^2 -x в точке x = -1

Question

Алгебра: Найти уравнение касательной для функции y =x ^2 -x в точке x = -1​

polina2004121 · Answer

Объяснение:Уравнение касательной от функции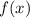 в точке 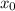имеет вид: 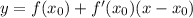.В нашем случае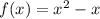 .Тогда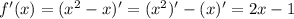 .Как указано,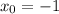 .Тогда уравнение касательной будет таким:...

Найти уравнение касательной для функции y =x ^2 -x в точке x = -1​