1. Алгебра
  2. Найти точку в которой функция

Найти точку в которой функция y=(6-x)e^10-x на отрезке 2; 9 принимает наименьшие значения

vikki17481 vikki17481    3   19.07.2019 00:40    1

Ответы
mityatimofeev mityatimofeev  03.10.2020 07:28
Возьмём от неё производную и приравняем нулю:
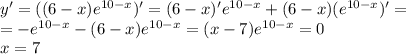
y'=((6-x)e^{10-x})'=(6-x)'e^{10-x}+(6-x)(e^{10-x})'=\\=-e^{10-x}-(6-x)e^{10-x}=(x-7)e^{10-x}=0\\x=7
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
макс3096 макс3096  25.11.2021 15:38
1.Запишите координаты вершины параболы a)y=-3x^2=11 b)y=(x+7)^2 2.изобразите схематически графики функций a)y=2x^2-2 b)y= -(x-6)^2 3.используя шаблон функции y=x^2,постройте...
Rozeta2003 Rozeta2003  18.11.2020 07:23
Заполните таблицу: очень надо по алгебре тотябы какое-то​...
dkcmvmcmf dkcmvmcmf  18.11.2020 07:23
Из некоторого пункта вышли одновременно два класса. Один класс направился на север, а другой — на восток. Спустя 4 ч. расстояние между ними было равно 24 км, причём первый...
svetaalekperova svetaalekperova  18.11.2020 07:24
Условие задания: Вычисли периметр треугольника ВС А и сторону BA, если CF — медиана,AC = ВС = 44 дм и BF = 16,5 дм.(Укажи длину и единицу измерения со строчной (маленькой)...
прп30 прп30  18.11.2020 07:24
2. В одной и той же системе координат постройте графики функций и найдите координаты точки пересечения прямых: у = 3-х и у = 2х. 3. а) Найдите координаты точек пересечения...
chiginavera chiginavera  18.11.2020 07:25
2+2+2+2+2+2+2+2+2+2+2+2+2+2+2+2+2+2+2+2+2+2+2+2+2+2+2+2+2+2+2= ШИТАЙТЕ РАЗДАЧА...
Ivan700 Ivan700  18.11.2020 07:26
При каком х значение вырожения х-2/3 на 2больше значентя вырожения х-3/2​...
Kolelove050 Kolelove050  18.11.2020 07:26
Привет ребят Решите вот ЭТО ВСЕ. Я не понимаю, я тупой...
axeltrofimsky axeltrofimsky  18.11.2020 07:35
Нужно найти первые 5 членов цепи...
arseniybox arseniybox  18.11.2020 07:35
Зная, что (xn) - арифметическая прогрессия и x1=4, x2=0,5, найдите : а) x5 б)x11 в)xk​...

Популярные вопросы