Найти точку минимума функции y=x^2+4x+26(всё в корне)

функция квадратного корня "хорошая" - ее минимум там же, где и минимум подкоренного выражения.

Под корнем квадратный трехчлен с ветвями, направленными вверх, тогда точка минимума одна и это - вершина

Вершина здесь при x=-4/2=-2

На всякий случай можно проверить, что подкоренное выражение в точке минимума положительно, но это и так очевидно.

ответ. -2.

Можно найти производную:

=(x^2+4x+26)'/2=2x+4/2

Приравняем к 0:

2x+4/2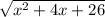=0

(2(x+2))/2=0

(x+2)/=0

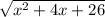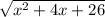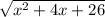т.е x+2=0 и =/0

x=-2

x^2+4x+26=/0 (корней нет)

(=/)-не равен 0.

ответ: x=-2