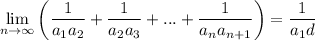Найти ) ,
,
где { } - арифметическая прогрессия, все члены и разность d которой отличны от нуля.
} - арифметическая прогрессия, все члены и разность d которой отличны от нуля.
Другие вопросы по теме Алгебра
Популярные вопросы
- 4. (0, ) Знайдіть площу трикутника МКР , иилцо МК в см,КР - 8 см,...
2 - Осы агылшын комектесндерши...
1 - Целое число или десятичная дробьсообщение учителю : 1центростремительное...
3 - сделать практическую на дальний восток...
3 - Пружина сжата и скреплена нитью. На пружинеежит алюминиевый кубик,...
1 - Где на земной поверхности формируются пояса низкого давления над СЕВЕРНЫМ...
1 - Установи відповідність: Між назвою та жанром твору: 1.Про Іллю Муромця...
2 - Від кінця 12ст. поширення набувають храми з одним куполом, пірамідальної...
1 - Заполни семантическую карту Есімдіктер Жіктеу Сілтеу Сұрау Өздік Болымсыздық...
3 - 1 Перенесению бактериями неблагоприятных условий ствуета) симбиоз...
1
Распишем сначала сумму для удобства и потом подсчитаем предел
Переходя к пределу при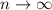 мы получим
мы получим
ответ: