Найти сумму всех целых a из промежутка [-3;15], при которых функция f(x)=lg((x²+3)×㏒0,5 a - 2x(2-㏒2 a)+4x²+6) определена на всей числовой оси объясните подробно у log числа 0,5 и 2 основания
Другие вопросы по теме Алгебра
Популярные вопросы
- Из 24м ткани сшили 8 платьев.сколько м ткани нужно для того,чтобы...
3 - Составить словосочетание со словом вдевая...
3 - Укажите такие точки графика функции y=x^2, абцисса каждой из которых...
2 - (6) предстояло строить здесь мирную жизнь, завязывать контакты с европой(где...
3 - При умножение двух однозначных чисел получилось число 12 какое число...
2 - Почему люди пишут вымасел в своих дневниках...
2 - Сочинение на тему какой ты след оставишь на земле с вопросами: все...
1 - Охариктирезуйте признаки при земноводных к жизни и на суше,и в воде...
3 - Вкорзине лежат 30 грибов: рыжики и грузди. известно, что среди любых...
2 - Составьте сказку рождение черешни в саду строчно надо...
2
6
Объяснение:
Область определения функции: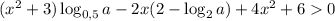 . Неравенство должно выполняться для любого x, в частности для x = 0. Подставим это значение:
. Неравенство должно выполняться для любого x, в частности для x = 0. Подставим это значение:
Значит, потенциально подходящие значения a = 1, 2, 3. Необходимо проверить каждое из них, чтобы удостовериться, что неравенство справедливо для всех x. Приведём левую часть к стандартному виду квадратного трёхчлена:
Так как a не превосходит 3, старший коэффициент положителен, ветви параболы направлены вверх. Значит, чтобы неравенство выполнялось для всех x, дискриминант левой части (или в данном случае удобно использовать D/4) должен быть отрицательным:
Пусть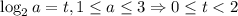 .
.
Все t подходят, а значит, и все a. Сумма подходящих a — 1 + 2 + 3 = 6.