Найти сумму. см. во вложении
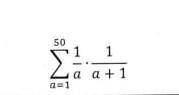
Другие вопросы по теме Алгебра
Популярные вопросы
- Исправьте текст, изменив порядок слов в приведённыхконструкциях.1. В субботу для...
3 - Исправьте предложения, устранив скопление одинаковых падежных форм в линейной последовательности.1....
3 - Такая ситуация. Нам задали сделать проект по любому предмету, по любой теме. У...
1 - АНГЛ. Поместите инфинитив в нужное время и составляйте предложения с COMPLEX SUBJECT...
3 - Составить рассказ о географическом положении Евразии и истории исследования материка,...
2 - Напишите структурные формулы следующих аминокислот: а) 3-аминопропановой кислоты;...
2 - Замените выделенные слова и словосочетания глаголами, которые пишутся с не слитно....
1 - АНГЛИЙСКИЙ. Exercise 5. Change these sentences using be likely , be unlikely ,...
3 - Составьте 4 вопроса на казахском по этому тексту)...
3 - таблица по географии 7 класс характеристики стран западной Европы 1 столбик: клим....
3
Объяснение:
Заметим, что
(1/a)(1/(a+1))=(1/a)-(1/(a+1))
Тогда
₅₀
∑ 1/(a(a+1)) = (1/1)-(1/2)+(1/2)-(1/3)+...+(1/49)-(1/50)+(1/50)-1/(51)=
a=1
=(1/1)-(1/51)=(51-1)/51=50/51