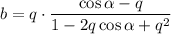Найти сумму ряда
[tex]qsina+q^2sin2a++q^nsinna+/tex]
Другие вопросы по теме Алгебра
Популярные вопросы
- 4. Рассмотри рисунок состава стали ( )ос- углерод 0,36 - 0.44si - кремний 0,17-0,37...
2 - решить физику. Задача с импульсом...
1 - Study the key phrases. Then say dates 1-6. Listen and check.KEY PHRASES O Dates20th...
3 - 1. Выберите функции, графики которых параллельны, ответ обоснуйте: A) у = 8 и у...
3 - Put the verbs from the brackets in the appropriate form. (Past Simple or Past Continuous)...
2 - Summative assessment for the unit Entertainment and Media * ОбязательноReadingTextRead...
2 - Только 3,4 и 5 Очень нужно ( )...
3 - Найти произведение корней уравнения: |2х-3|=8...
2 - – 5 * 3 =9 *(– 3) = – 10 * (– 8) =– 55 : 11 =...
2 - 11. Вместо многоточий, допиши Климатические пояса делятся на……, их различие в том,...
1
Пусть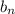 и
и 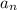 - последовательности частичных сумм первого и второго, соответственного и b , a - их суммы.
- последовательности частичных сумм первого и второго, соответственного и b , a - их суммы.
По формуле Эйлера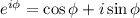 , мы получим
, мы получим
Здесь в этом случае бесконечно убывающая геометрическая прогрессия.
Преобразовывая в тригонометрическую форму по формуле Эйлера, мы получим
Откуда искомая сумма ряда