Найти сумму корней уравнения 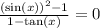, принадлежащих отрезку [0; π] .Заранее

Question

Алгебра: Найти сумму корней уравнения , принадлежащих отрезку [0; π] .Заранее

ilinasmirnova5 · Answer

ответ: sin²(x)-1=0⇒sin²(x)=1⇒sin(x1)=1⇒x1=π/2

sin(x2)=-1⇒ нет корней на заданном интервале

1-tg(x)≠0⇒x≠π/4. Также значение tg(π/2) не определено и поэтому х≠π/2. Таким образом, на заданном интервале корни отсутствуют, их сумма равна нулю.

Объяснение:

Найти сумму корней уравнения $\frac{ {(\sin(x) })^{2} - 1}{1 - \tan(x) } = 0$
, принадлежащих отрезку [0; π] .

Заранее