Найти сумму бесконечной убывающей геометрической прогрессии

Другие вопросы по теме Алгебра
Популярные вопросы
- Как такое решать? решите с объяснением 1/6-2/3...
3 - Марьяна (звуко-буквенный разбор) полный...
1 - Хто в османській імперіі мав титул халіфа? а) правитель б) голова уряду...
2 - Деятели москвы. их главные вклады в )...
2 - Сколько стоит 1 апельсин если 4 стоят 20 рублей...
1 - Пример на пословицу кашу маслом не испортишь...
1 - Перевести текст с : in 1974 , a group of farmers in china were digging...
2 - Разложение гидрооксид цинка 8 класс...
2 - Синтаксический разбор слова по сторонам...
2 - Почему влажные экваториальные леса имеют такой разнообразный видовой...
3
Найдём знаменатель геом. прогрессии: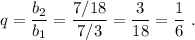
Проверим: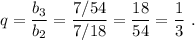
Так как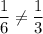 , то задана не геометрическая прогрессия .
, то задана не геометрическая прогрессия .
P.S. А формула суммы бесконечно убывающей геометрической
прогрессии такая: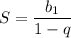 .
.