Найти сумму 22 первых членов арифметической прогрессии 25,30,35,
Другие вопросы по теме Алгебра
Популярные вопросы
- Какие регионы Казахстана получают больше солнечной радиации? Почему?....
3 - Каковы итоги политики первых Московских князей?...
3 - Прочитай текст. По моему мнению, люди изучают иностранные языки, потому что...
1 - Увеличь в 7 раз. 8.6.9.4.3.1...
1 - 4. Ana oğluna hansı tərbiyəvi xüsusiyyətləri aşılayır? Aşağıdakı cədvəli tamamlamaqla...
1 - 1.-Что Вы знаете о Рождестве, о смысле этогопраздника?...
1 - Тело проходит 5 одинаковых участков пути, имея различные скорости: первый участок...
3 - 2 варіант Виберіть одну правильну відповідь (по 0, ) 1. Укажіть організм, що...
2 - Составьте визитную карточку IT-генетика. Включите в неё указанную информацию...
2 - Какие из следующих формул задают в функцию у от x, а какие нет 1)у= - 3 x +...
3
(an) - арифметическая прогрессия
а1=25, а2=30, следовательно d=a2-a1=5,
из формулы суммы первых n членов арифметической прогрессии находим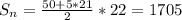
а1=25
а2=30
а3=35
а4=40
найти S(22)=?
d=a(n+1)-a(n)=a2-a1=30-25
d=5
S(n)=((2*a1+d*(n-1))/2)*n
S(22)=((2*25+5*21)/2)*22=((50+105)/2)*22=(155/2)*22=155*11
S(22)=1705