НАЙТИ ПРОИЗВОДНЫЕ (КРОМЕ ПЕРВЫХ ДВУХ) все что сможете сами решить
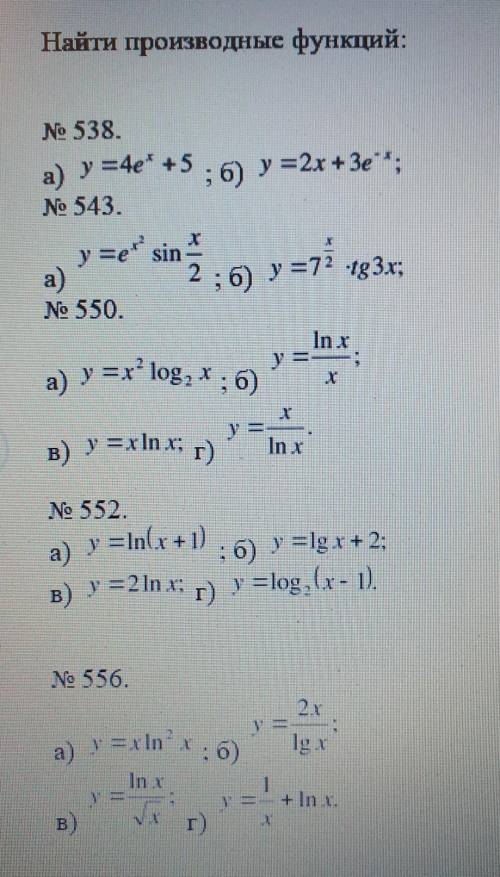
Другие вопросы по теме Алгебра
Популярные вопросы
- 1 Match the sentences with their tenses. 1) I ll bring your book back tomorrow....
3 - Сочинение Тема любви в русской поэзии...
2 - Зразок металу, з МЕ = 29,355 г/моль, при взаємодії з кислотою утворює 105...
3 - Мой профиль Выйти Условие задания: 25. В Максим собирался купить 30 конфет(-ы),...
1 - 1.109. Представьте выражение в виде степени с основанием 3: 1) 3 -3n+1.31-n,...
2 - напиши в правильном порядке имена ветхозаветных праведников ,которые стали...
1 - Из стихотворения Державина Памятник выписать сложные предложения...
2 - Сократите дробь 20/33. Лёгкие очки...
1 - Навести приклади використання: 1. Форматів %e і %g у функціях printf і...
3 - Талдау Қорқыттан қалған нақыл сөздерді мазмұндас мақал-мә телдермен салыстырып,...
1
543
а)
б)
550
а)
б)
в)
г)
552
а)
б)
в)
г)
556
а)
б)
в)
г)