Найти производную функции
y=(2x^3-1)/x+5
Другие вопросы по теме Алгебра
Популярные вопросы
- Make video about fashionдайте текст , что мне сказать на видео...
3 - Сары тауык пен балапандары...
3 - решить діаметр кола. Знайти координати центра кола, якщо A(-3; 2). B(3; 7); a)...
3 - Правильно ли я сделала тут нужно подчеркнуть обособленные члены только правильно...
1 - Написати твір на тему “Ми діти твої, природо!”, використовуючи лише складні речення....
2 - В каком из трех состояний вещества при одной и той же температуре диффузия происходит...
1 - Из перечня (1-23) выберите наиболее полные ответы на вопросы1. Кости стопы2. Кости...
2 - Переведи данную скорость в указанные единицы измерение 2107 км/ч = ? М/мин результат...
2 - решить 2 задачи по физике, очень сложно.. 1) два одинаковых заряда отталкиваются...
3 - F(x)=-x^4+4x^2-3 найдите интервалы монотонности и экстремумы функции....
1
(..) это означает производное вы будете поставить ( ' )
y=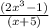
y' =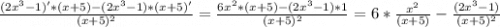
посчитано по формуле (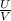 )'
)'