Найти производную функции y=√(2x^2 -3)^9
Ответы
Используем правила дифференцирования сложной функции и степенной функции:
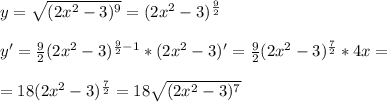
ПОКАЗАТЬ ОТВЕТЫ
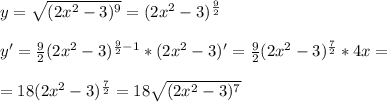
Другие вопросы по теме Алгебра
Популярные вопросы
- Визначте відносну вологість повітря якщо в одному метрі кубічному...
1 - Имеется 9кг крупы и чашечные весы с гирями в 50г и 200г. попробуйте...
1 - Определить причины и последствия крестовых походов...
1 - :в организме произошла мутация. полипептидная цепь обрывается в...
3 - Please (желательно модераторы либо тот кто шарит) как пересказать...
2 - Протон влетает в однородное электрическое поле со скоростью 200км/с...
2 - Сшумом и хлопаньем вылетают из зарослей птичьи стаи синтаксический...
2 - Скакими из перечисленных веществ s,h2so4,kcl,hq (no3)2 может взаимодействовать...
2 - Инструкцию к любому действию (как сварить суп, как вырастить цветок,...
3 - Катя завоевала 13 медалей золотых и серебряных причём серебряных...
1