1. Алгебра
  2. Найти производную функции

Найти производную функции при данном значении аргумента 1 f(x)=sin²x, при x= п/4. 2 f(x)=lncosx, при x= -п/3. 3 f(t)=sint-cos² t, при t=0. 4 f(z)=ln tg z, при z=п/4.

МАШЕНЬКА881 МАШЕНЬКА881    1   22.05.2019 02:30    0

Ответы
380973599293 380973599293  17.06.2020 03:06

1)y=sin^2x

 y'=(sin^2x)'=2sinx(sinx)'=2sinx*cosx=sin2x

 x=\frac{\pi}4= y'(\frac{\pi}4)=sin\pi=0

 2)y=lncosx

 y'=(lncosx)'=\frac{1}{cosx}*(cosx)'=-\frac{sinx}{cosx}=-tgx

 x=-\frac{\pi}3=y'(-\frac{\pi}3)=-tg(-\frac{\pi}3)=tg(\frac{\pi}3)=\sqrt{3}

 3) y=sint-cos^2t

 y'=(sint-cos^2t)'=(sint)'-(cos^2t)'=cost-2cost(cost)=

 =cost+2cost*sint=cost+sin2t

 t=0=y'(0)=cos0-sin0=1-0=1

 4) y=lntgz

 y'=(lntgz)'=\frac{1}{tgz}(tgz)'=\frac{\frac{1}{cos^2z}}{tgz}=\frac{\frac{1}{cos^2z}}{\frac{sin^2x}{cos^2x}}=\frac{cos^2x}{sin^2xcos^2x}=\frac{1}{sin^2x}

 z=\frac{\pi}4=y'(\frac{\pi}4)=\frac{1}{sin^2(\frac{\pi}4)}=\frac{1}{\frac{2}{4}}}=\frac{4}2\2

ПОКАЗАТЬ ОТВЕТЫ
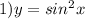
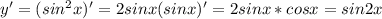
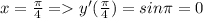
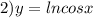
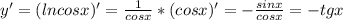
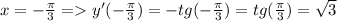
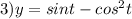
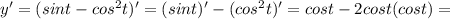
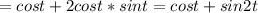
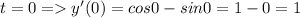
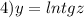
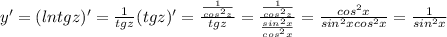
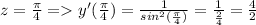
Другие вопросы по теме Алгебра
gentleman2 gentleman2  02.08.2019 00:40
Разложить на множители 4х^2-2ху 4ху^2+4у^3 4х^2-у^2 12х^2-3у^2 ху^2-4х^3 4х^2-4ху+у^2 -х^2-4ху-4у^2 х^2у-4ху^2+4у^3 3х^3-3у^3...
GlebRyabov GlebRyabov  02.08.2019 00:40
Из городов а и б, расстояние между которыми равно 360 км, навстречу друг другу одновременно выехали 2 автомобиля и встретились через 3 часа на расстоянии 195 км/ч...
AGIDELKA2004 AGIDELKA2004  02.08.2019 00:40
Найдите наименьший корень уравнения x^3-49x=0...
oomasha oomasha  02.08.2019 00:40
X^{2} +2ax-3a^{2} =0 розв*язати рівняння...
kiss123kiss kiss123kiss  02.08.2019 00:40
4целых 5/6 - 5/8 - 2 целых 1/4 * 1/6...
лерчик1253 лерчик1253  02.08.2019 00:40
Числитель 2у²+7у+3 знаменатель у²-9...
Полинка1608 Полинка1608  02.08.2019 00:40
С( нужно составить уравнение): путь от пункта а до пункта в поезд преодолел за 3 часа. за первый час он проехал 30% всего пути, за второй час 5/6 пути, пройденного...
Саша555111 Саша555111  02.08.2019 00:40
Изобразите схематически график функции y=-5(2-|x|)^1/2...
DjYuLiAnNa DjYuLiAnNa  02.08.2019 00:40
Решите : 1) (4x-3)²-6x(4-x). 2) (p+3)(p-11)+(p+6)². 3) (a-x)²+(a+x)². 4) 2(x+6)²-(20x+70)...
xXEliteXx xXEliteXx  17.12.2020 15:01
Знайдіть для функції f(x) = 2x − 6x 2 − 4x 3 первісну, графік якої проходить через точку A(−1; −3)....

Популярные вопросы