1. Алгебра
  2. Найти производную функции

Найти производную функции 11 класс, повышенная сложность. f(x) и g(x) непрерывны и дифференцируемы.

саша2006101 саша2006101    2   06.09.2019 13:00    0

Ответы
adyan22041996 adyan22041996  26.08.2020 16:24
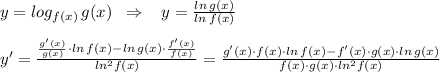
y=log_{f(x)}\, g(x)\; \; \Rightarrow \; \; \; y= \frac{ln\, g(x)}{ln\, f(x)} \\\\y'= \frac{\frac{g'(x)}{g(x)}\cdot ln\, f(x)-ln\, g(x)\cdot \frac{f'(x)}{f(x)} }{ln^2f(x)} = \frac{g'(x)\cdot f(x)\cdot ln\, f(x)-f'(x)\cdot g(x)\cdot ln\, g(x)}{f(x)\cdot g(x)\cdot ln^2f(x) }
ПОКАЗАТЬ ОТВЕТЫ
btrawee34 btrawee34  26.08.2020 16:24
Сначала логарифм приведём к натуральному основанию, а затем по формулам дифференцирования частного и сложных функций.

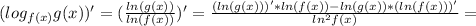
(log _{f(x)} g(x))'= (\frac{ln(g(x))}{ln(f(x))} )'= \frac{(ln(g(x)))' *ln(f(x))-ln(g(x))*(ln(f(x)))'}{ln ^{2}f(x) } =

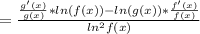
= \frac{ \frac{g'(x)}{g(x)}*ln(f(x))-ln(g(x))* \frac{f'(x)}{f(x)}}{ln ^{2}f(x) }
ПОКАЗАТЬ ОТВЕТЫ
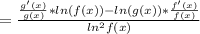
Другие вопросы по теме Алгебра
марс56 марс56  19.06.2019 05:20
Найти корень уравнения. 1, 8x/9=-16/9 2, 3a-132/13+4=-8 3,3c/5=-6/5 4,3d-31/5=-2 5,184-4y/8+18=37...
artur17499 artur17499  19.06.2019 05:20
Разложите на множители многочлен 1) ах-ау+zх-zу , 2)х^2-ху-6х+6у. 2) выполните умножение многочлена на многочлен (х+у) (у+п) , (2-у) (3у-8) (4а^2+b^2)...
машана1 машана1  19.06.2019 05:20
Для приготовления фарша взяли говядину и свинину в отношении 31: 19. какой процент в фарше составляет свинина?...
Егор200417 Егор200417  19.06.2019 05:20
Найдите знаменатель прогрессии если 1)b1=1,b4=64. 2)b6=25,b8=9. решите с подробностями...
dddashaaa1 dddashaaa1  19.06.2019 05:20
Выражение: 1) (m+4)^2-(m-3)(m+3) 2) 3(b-1)^2+8b 3) (n+5)^2-n(n-7) 4) 2c(8c-3) -( 4c+1)^2...
rdutchik rdutchik  19.06.2019 05:20
Log6(x+7)=log6(6x-13) log2(8+3x)=log2(3-x)+1...
krisdenya2005 krisdenya2005  19.06.2019 05:20
Оптовая стоимость сд - диска 60 руб. при покупке от 50 до 70 дисков предоставляется скидка 3%, при покупке более 70 дисков предоставляется скида 5%. сколько будут...
AleksandrYamaha AleksandrYamaha  19.07.2019 22:00
Нужна : найдите знаменатель прогрессии 7, 1/√7, 1/49...
Викатульская Викатульская  19.07.2019 22:00
Найдите последнюю цифру в значении выражения 17^2+13^3+2*3*4**88...
vjvxjbnkgsvjsvs vjvxjbnkgsvjsvs  19.07.2019 22:00
Сократите дробь ( a+5)^2/a^2-25 надо...

Популярные вопросы