Найти предел функции.
Правила Лопиталя применять нельзя
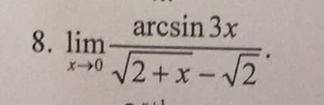
Другие вопросы по теме Алгебра
Популярные вопросы
- Вірш на тему ініціативність ...
1 - Какие правильные ответы в 4 задании очень у меня тест завтра...
1 - Чому людина може втратити здатність розрізняти ті або інші подразнення?...
2 - Чому сенсорні системи називають аналізаторами ?...
3 - Что значит давать выигрыш (проигрывать) в чем-то (в работе,...
3 - составьте цитатную таблицу лонгрен и жители каперны душевные...
2 - Можно ли жить без Родины : Родина имеет для каждого из нас...
2 - точка М належить бісектрисі CD рівнобедреного трикутника ABC...
1 - ответить на вопросы 6-го задания...
1 - ОЧЕНЬ НУЖНО Рассчитайте годовую амплитуду температур воздуха...
1
Но мы представим 1 как дробь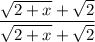 , такое действие еще называют домножением на сопряжённое
, такое действие еще называют домножением на сопряжённое
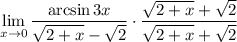
3 Соберем все в одну дробь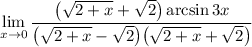
4 Заметим в знаменателе разность квадратов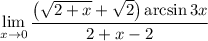
5 Упростим знаменатель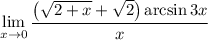
6 Представим дробь как произведениеНо 1 мы представим в виде
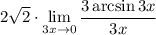
11 Вынесем константу (3) за предел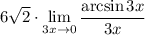
12 Имеем первый замечательный предел, он равен 1