Алгебра: Найти площадь фигуры, ограниченную линиями y=-x^3, y=-x

Найти площадь фигуры, ограниченную линиями y=-x^3, y=-x

Ответы

Мальвина01 15.10.2020 14:49

Решение:

Большое количество задач такого типа решаются при формулы Ньютона-Лейбница:

$\displaystyle \int\limits^b_a {f(x)} \, dx = F(b) - F(a)$

Поэтому, во-первых, нужно найти и 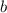- абсциссы точек пересечения графиков функций. Для этого нужно решить несложное уравнение:

$-x^3 = -x\\\\x^3-x=0\\\\x \cdot (x^2-1)=0\\\\\Rightarrow \; x_1 = -1, \; x_2 = 0, \; x_3 = 1$

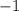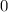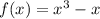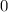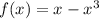А так как есть целых три точки пересечения, то придется считать два интеграла: первый - от до (как результат приравнивания функций: f(x) = x^3-x ), а второй - от до (здесь уже f(x)=x-x^3 ):

$\displaystyle \int\limits^0_{-1} {\Big (x^3-x \Big) } \, dx + \int\limits^1_{0} {\Big (x-x^3 \Big) } \, dx = \bigg ( \frac{x^4}{4} - \frac{x^2}{2} \bigg ) \Big | ^0_{-1} + \bigg ( \frac{x^2}{2} - \frac{x^4}{4} \bigg ) \Big | ^1_{0} =\\\\= \bigg ( \Big (\frac{0}{4} - \frac{0}{2} \Big ) - \Big (\frac{1}{4} - \frac{1}{2} \Big ) \bigg ) + \bigg ( \Big (\frac{1}{2} - \frac{1}{4} \Big) - \Big (\frac{0}{4} - \frac{0}{2} \Big ) \bigg ) = 2 \cdot \bigg (\frac{1}{2} - \frac{1}{4} \bigg ) = \frac{1}{2}$

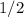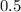Значит, площадь искомой фигуры (состоящей из нескольких других фигур) равна 1/2 или 0.5 (каких-то квадратных единиц измерения), если перевести в десятичную дробь.