Найти площадь фигуры: f(x)= x в квадрате - 8x+18 y=-2x+18

Question

Алгебра: Найти площадь фигуры: f(x)= x в квадрате - 8x+18 y=-2x+18

Nosochekxnncnnc · Answer

Чтоб решить задание сначала ножно нарисовать график функции и линию. Сначала функцию x^{2} -8х+ 18 . Для этого ищем Х вершину и У вершину. Х вершина =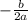 $-\frac{b}{2a}$ где b=-8 а а=1. когда подставили то Хв будет равна 4. чтоб найти У вершину то нужно это 4 поставить в x^{2} -8х+ 18 и тогда У вершина= 2. нужно дальше найти точки касания графика с Ох то есть функцию прировнять к 0. если все посчитать то выйдет что D<0 то есть график не соприкасается с Ох.. Поэтому чтоб понять в каких точках соприкасается y=-2x+18 и f(x)= [x^{2} -8х+ 18 нужно их прировнять то есть:

-2x+18=x^{2} -8х+ 18 -8х+ 18 и тогда с этого выйдет x^{2} - 6х=0 отсюда выносим х и выходит х(х-6)=0 тогда х=0 и х=6.

$\int\limits^6_0 {(-2x + 18 - x^{2} + 8x - 18)} \, dx = \int\limits^6_0 {(6x - x^{2})}\, dx= 3x^{2} - \frac{x^{3}}{3}$ = 108- $\frac{216}{3}$ = 108-72=36

Найти площадь фигуры: f(x)= x в квадрате - 8x+18 y=-2x+18

Популярные вопросы