1. Алгебра
  2. Найти площадь боковой поверхности

Найти площадь боковой поверхности правильной четырёхугольной пирамиды,сторона основания которой равна 16 и высота равна 6

К5О5Т5 К5О5Т5    3   15.03.2020 14:36    1

Ответы
Valeriya2576 Valeriya2576  11.10.2020 22:07

320 см²

Объяснение:

Правильная четырёхугольная пирамида - это пирамида, основание которой - квадрат. Площадь боковой поверхности любой правильной пирамиды вычисляется по формуле:

S = \frac{n\cdot a}{2} \sqrt{h^2 + (\frac{a}{2tg(\frac{180^\circ}{n})})^2}, где a - сторона основания, n - число сторон основания, h - высота пирамиды.

В нашем случае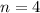 n = 4, так как основание квадрат.

S_{ABCD} = \frac{16\cdot4}{2} \cdot \sqrt{6^2 + (\frac{16}{2tg(\frac{180^{\circ}}{4})})^2} = 16\cdot 2 \cdot \sqrt{6^2 + (\frac{16}{2tg(45^{\circ})})^2} = 32\cdot \sqrt{36+(\frac{16}{2})^2} =\\\\32 \cdot \sqrt{36 + 64} = 32 \cdot \sqrt{100} = 32 \cdot 10 = 320cм²

ПОКАЗАТЬ ОТВЕТЫ
daниил1 daниил1  11.10.2020 22:07

ответ: во вложении Объяснение:


Найти площадь боковой поверхности правильной четырёхугольной пирамиды,сторона основания которой равн
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
123Настенька 123Настенька  30.09.2019 10:10
Постройте график функции y=x^2-6x+9 !...
SleepWalker5669 SleepWalker5669  30.09.2019 10:10
Укажите наибольшее и наименьшее целое число, принадлежащее промежутку 1) [-10; -5] 2) (6; 12)...
Никитаотличник1 Никитаотличник1  30.09.2019 09:13
Вгороде n было два. магазина . изначально в первом было 84 кг мяса . во втором 96 кг. ежедневно первый магазин продавал по 12 кг мяса. а второй по 21 кг мяса. через сколько...
КристинаМельникова КристинаМельникова  30.09.2019 10:10
Янашла вершину ,но получилось много и я не знаю как это начертить.вершина (5; -16),ветви параболы направлены вверх,так как а≠0 постройте график параболы. -х²+10х+9...
lilia104 lilia104  06.10.2019 14:40
#1a^3+b^6x^6+y^6p^3-q^9#2x^3y^3+1a^3c^3-b^3a^3b^3+64#3(ab-4)(a^2b^2+4ab+16)(2a-b/2)(4a^2+ab+b^2/4)#4a^3b^6-c^312am^3-12an^31-p^9pls help!...
alinavinokutov alinavinokutov  06.10.2019 14:40
Найдите наибольший отрицательный корень уравнения ctg πx/8 = -1...
Myrzik007 Myrzik007  06.10.2019 14:40
Найти экстремум y＝x∧3+10x∧2+10 найти у наиб. и у наим. y＝x∧3-3x+10 [-3，2]...
zac00 zac00  06.10.2019 14:40
Объясните с подробным решением данного примера...
angelinachka3000 angelinachka3000  06.10.2019 14:40
Укажіть пару чисел, яка є розв язком рівняння x+y=25...
smolekovmax smolekovmax  06.10.2019 14:30
Ac-cx-ab+bx-a+x представьте многочлен в виде произведения...

Популярные вопросы