1. Алгебра
  2. Найти остаток от деления 23^34+56^67

Найти остаток от деления 23^34+56^67 на 9

belos1988 belos1988    3   27.08.2022 14:19    12

Ответы
stentani97 stentani97  27.08.2022 14:20

Два числа называются равными по модулю N, если одно из них получено путем прибавления к другому (или вычитания от другого) некоторого количества раз числа N:

A\equiv A+kN\pmod{N},\ k\in\mathbb{Z}

Свойство равенства по модулю:

A^B\equiv (A+kN)^B\pmod{N},\ k\in\mathbb{Z}

Числа, равные по модулю N, дают при делении на N равные остатки.

Преобразуем первое слагаемое:

23^{34}=(-4+3\cdot9)^{34}\equiv(-4)^{34}=4^{34}=2^{68}=2^2\cdot2^{66}=4\cdot(2^3)^{22}=4\cdot8^{22}=

=4\cdot(-1+9)^{22}\equiv4\cdot(-1)^{22}=4\cdot1=4\pmod{9}

Преобразуем второе слагаемое:

56^{67}=(2+6\cdot9)^{67}\equiv2^{67}=2\cdot2^{66}=2\cdot(2^3)^{22}=2\cdot8^{22}=

=2\cdot(-1+9)^{22}\equiv2\cdot(-1)^{22}=2\cdot1=2\pmod{9}

Тогда:

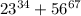23^{34}+56^{67}\equiv4+2=6\pmod{9}

Число 23^{34}+56^{67}, также как и равное ему по модулю 9 число 6, дает при делении на 9 остаток 6.

ответ: 6

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
kif1305 kif1305  03.04.2020 00:53
Разложи число 2548 на множители. (Множители записывай в порядке возрастания; если множитель встречается несколько раз, то запиши его в виде степени!)...
анч21 анч21  03.04.2020 00:53
Знайди точку перетину прямих y=3x+15 і y=-7x+15, не виконуючи побудови графіків...
Lizaforever11 Lizaforever11  03.04.2020 00:54
У выражение -0.81z6 кв в корне, если z 0...
катя5088 катя5088  03.04.2020 01:01
Представьте в виде многочлена стандартного вида. 1) а) (х+2)^2=?б) (2a+3b) ^2=? в) (5x-7) ^2=? г) (4a-b) ^2=? 2) а)(m+4) ^2=? б)(3m+2n) ^2=? в) (7m-2) ^2=? г)(8m-n)...
778392 778392  03.04.2020 01:00
Стадіон має чотири входи: А, B,C і D. Скільки існу в увійти через один вхід, а вийти через інший? *​...
мадина523 мадина523  03.04.2020 01:05
Если подбросить мяч вертикально вверх, то высота (h), на которой находится мяч через (t) секунд полета вычисляется по формуле h(t)=-3t^2+6t a)через сколько секунд...
DaniilF3001 DaniilF3001  15.03.2021 12:55
Вынесите за скобки общий множитель (а-с)у+(с-а)z ay-cy+cz-az (a-c)(y-z) (a-y)(c-z) (a-c)(y+z) СОЧ ПО АЛГЕБРЕ...
Alexsandra2195 Alexsandra2195  15.03.2021 12:55
дам 40 или больше балов только делайте сами в интернете другие примеры ​...
magnoliya220619 magnoliya220619  15.03.2021 12:55
Для заданной функции 1 (x) = - (x-3) ² + 12: а) определить плоскость параболы б) определить ось симметрии параболы в) найти точку пересечения с осью OX д) найти точку...
qwerty999999fgh qwerty999999fgh  15.03.2021 12:55
Разложите на множители a)x² -81 б)y² -4y+4 в)(x-1)² +(x+1)²...

Популярные вопросы