Найти остаток от деления: 1) числа 39^46 на 5; 2) числа 64^29 на 7; 3) числа 103^15 на 17; 4) числа 10^10 + 28^3 - 1 на 3; 5) числа

Question

Алгебра: Найти остаток от деления: 1) числа 39^46 на 5; 2) числа 64^29 на 7; 3) числа 103^15 на 17; 4) числа 10^10 + 28^3 - 1 на 3; 5) числа 7*10^30 на 9

соня3161 · Answer

Заметим, что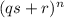 (qs+r)^n дает такой же остаток при делении на s, что и 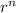r^n . (Доказывается, например, так. Раскрываем скобки:

$(qs+r)^n=qs(qs+r)^{n-1}+r\cdot(qs+r)^{n-1}=qs(qs+r)^{n-1}+\\qs(qs+r)^{n-2}+r^2\cdot (qs+r)^{n-2}=\cdots=qs(\cdots)+r^n$

Очевидно, на каждом шаге будет образовываться слагаемое, делящееся на qs, и степень умноженная на r. Все слагаемые первого типа на остаток не влияют, так что остается только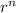 r^n )

Кроме того, остаток от деления от суммы равен остатку от деления от суммы остатков (as + b + cs + d = (a + c)s + (b + d) дает такой же остаток при делении на s, что и b + d), а так же произведение можно менять на произведение остатков

Применяем наблюдения:

$39^{46}=(40-1)^{46}\equiv (-1)^{46}=1\pmod{5}\\64^{29}=(63+1)^{29}\equiv1^{29}=1\pmod7\\103^{15}=(102+1)^{15}\equiv1^{15}=1\pmod{17}\\10^{10}+28^3-1=(9+1)^{10}+(27+1)^3-1\equiv1+1-1=2\pmod3\\7\cdot10^{30}=7\cdot(9+1)^{30}\equiv7\cdot1=7\pmod9$

Найти остаток от деления: 1) числа 39^46 на 5; 2) числа 64^29 на 7; 3) числа 103^15 на 17; 4) числа 10^10 + 28^3 - 1 на 3; 5) числа 7*10^30 на 9

Популярные вопросы