1. Алгебра
  2. Найти общее решение диференц.урав.

Найти общее решение диференц.урав. у"-6у'+9у=0​

тот22 тот22    3   16.06.2021 12:02    0

Ответы
swietajakubiak swietajakubiak  16.07.2021 12:05

Стандартный решения такого уравнения - с характеристического уравнения k²-6k+9=0; k=3 - кратный корень;

y_1=e^{3x};\ y_2=xe^{3x};\ y=C_1e^{3x}+C_2xe^{3x}.

Однако в простых случаях ответ можно получить без всякой теории. В данном случае, домножив уравнение наe^{-3x}, можем записать его в виде

(ye^{-3x})''=0;\ (ye^{-3x})'=C_1;\ ye^{-3x}=C_1x+C_2;\ y=C_1xe^{3x}+C_2e^{3x}

ПОКАЗАТЬ ОТВЕТЫ
roksi100200 roksi100200  16.07.2021 12:05

Смотри решение.

Объяснение:

1. Запишем уравнение в исходном виде:

y"-6y'+9y=0\\

2. Запишем характеристическое уравнение:

λ^2 - 6λ + 9 = 0

3. Решаем его через дискриминант:

a=1; b=-6; c=9\\D=(-6)^2-4*1*9\\D=36-36\\D=0\\\sqrt{D}=\sqrt{0}=0\\

4. Находим λ:

λ_1 = λ_2 =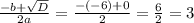 \frac{-b+\sqrt{D}}{2a}=\frac{-(-6)+0}{2}=\frac{6}{2}=3\\

5. Записываем общее решение данного дифферинциального уравнения:

Y_{obsch}=C_{1}e^{3x}+C_{2}e^{3x}\\

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
andreewnamap0c5nx andreewnamap0c5nx  23.04.2021 20:55
1) (3xx + 5)2(2xx − 5) 0; 2) 9xx2 − 6,25 0 ; 3) (3 − xx)(2xx + 3)2(3xx + 4) 0; 4) 4xx2 − 1,21 0 ; 5 ) (2xx + 5)2(3xx + 1)(2 − 3xx) 0; 6) 4xx2 − 1,44 0 ; хелп...
asiadancer asiadancer  23.04.2021 20:57
У фігуру, обмежену лініями у=х^2 та у=2х^2; х=6, вписан паралелограм найбільшої площини так, що дві його вершини лежать на прямій х=6, а дві інші- на параболах...
pro00losk pro00losk  23.04.2021 21:03
Упростите выражение:(5m/m+3-14/m²+69):5m+1/m²-9+3(m-3)/m+3​...
Legend1111111 Legend1111111  23.09.2019 04:10
Пропустил много тем из-за болезни. решите разложите на множители 1) 5ab+5xb 2) 2xy-8y 3)7a+21ay 4)9x^2-27x 5)3a-9a^2 6)5c^8-5c^7+10c^4 7)8p^7-4p^5+10p^3 8)3x(b-2)+y(b-2)...
Thandey Thandey  23.09.2019 04:10
Решите систему уравнений двумя...
sashashola sashashola  23.09.2019 04:10
Найти двух цифровое число, если число его единиц на 2 больше от числа десятков; если умножить искомое число на сумму его цифр то получим 144....
eruder eruder  23.09.2019 04:10
Фабрика выпускает сумки. в среднем 14 сумок из 140 имеют скрытые дефекты. найдите вероятность того, что купленная сумка окажется без дефектов....
Anyazz Anyazz  23.09.2019 04:10
F(x)=sin3x найдите первообразную график который проходит через точку m(п12; 0) !...
shabanovkirillp02mew shabanovkirillp02mew  02.10.2019 05:40
Применяя разложения на множители, найдите значение выражения (10^6*5^3-2^6)/10^6+10^3*2^3+2^6...
kosenaalina kosenaalina  02.10.2019 05:40
Решите уравнение a)1/3x=12 б)5x-4,5=3x+1,5 в)4x-6(x-1)=8+4(x-1) г)x/4+x+1/6=5 полный ответ ! заранее от души 3...

Популярные вопросы