Найти область значения функции 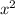+2x-8

Объяснение:

х²+2x-8=(х+1)²-9

(х+1)²≥0⇒(х+1)²-9≥-9

х²+2x-8≥-9

Так как коэффициент при x² > 0, значит ветки параболы направлены вверх, т.е. функция ограничена снизу и не ограничена сверху.

Найдем вершину параболы:

x₀ = -b/2a = -2/2 = -1

y₀ = f(x₀) = (-1)²+2(-1)-8 = 1-2-8 = -9

Значит, вершина параболы находится в точке (-1; -9) и область значения функции x²+2x-8 будет следующей:

E(y) = [-9; +∞).

ответ: E(y) = [-9; +∞).