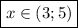Найти область сходимости ряда.
Другие вопросы по теме Алгебра
Популярные вопросы
- 45 кг : 5 1 дм 2 см : 6 6 см 3 мм : 9 27 г : 3 4 дм 8 см : 6 36 ц : 4...
3 - Сравнить средневековую деревню, и средневековый город (сходства и различия)...
3 - Написать 5 6 предложений про учителя на каз яз...
3 - Выписать 3 предложения из повести барышня -крестьянка в которых подлежащие...
3 - Как относится хлестаков к жене и дочери городничего?...
1 - Найди те части текста в которых природа думает,говорит и дейстувет как...
1 - Вырази в указанных еденицах изменениях 20см=? мм 1170см=? м? дм 180мин=?...
2 - 1дециметр 4 сантиметра сколько это будет...
2 - ответ жан-жака руссо на его обращение к людям...
1 - Откуда экосистема получает всё остальное, что нужно для жизни...
2
Итак, у нас есть ряд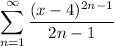 .
.
Вычислим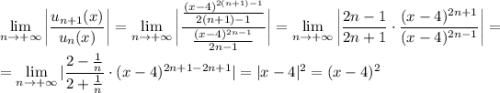
Вот это уже хорошо. Нужно, чтобы это выражение было меньше единицы (это из признака Даламбера), тогда мы найдем те самые х, при которых ряд будет сходиться.
Вот мы их получили. Но теперь нужно проверить концы: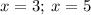
Что можно сказать об этом ряде? Допустим, мы будем использовать предельный признак сравнения. Есть известный ряд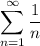 , он расходится, при этом предел отношения n-ых членов полученного ряда и приведенного не равен 0, а равен конкретной константе (-1/2, если делить n-ый член полученного на n-ый член ряда 1/n), так что при
, он расходится, при этом предел отношения n-ых членов полученного ряда и приведенного не равен 0, а равен конкретной константе (-1/2, если делить n-ый член полученного на n-ый член ряда 1/n), так что при 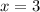 ряд расходится.
ряд расходится.
Аналогичная история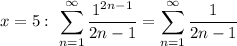
Все те же рассуждения, только предел отношения будет равен 1/2. То есть при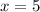 ряд расходится.
ряд расходится.
ответ: