Найти неопределённый интеграл методом замены переменной 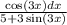
Другие вопросы по теме Алгебра
Популярные вопросы
- Почему социальные проблемы остаются острыми в нашем обществе? только, ,...
2 - Составить небольшие диалоги со всеми вопросов. (закрытые, открытые, прямые,...
1 - Написать в квадратики номер подходящего к понятию определения периодические...
2 - 90 і запишіть 5 речень з омонімами з художньої літератури. тобто щоб було...
1 - Уровнение по действиям 2 *(5+x)-2x=10 *-это умножение...
3 - Объясните, как осуществляется радиосвязь между двумя пунктами...
2 - 1)укажите предложение в котором допущена ошибка в постановке знаков препинания...
1 - Слова в предложениях перепутались! составь вопросительные предложения из...
1 - Репортаж по картине детская спортивная школа ! надо...
3 - Каково наименьшее возможное число участников кружка, если в нём чётное число...
1
Объяснение:
ПОДСТАВИМ ДИФФЕРЕНЦИАЛ, ИСПОЛЬЗУЯ "dx=1/t'*dt", ГДЕ "t=5+3sin(3x)" И "t'=3cos(3x)*3":
∫cos(3x)/(5+3sin(3x))*1/(3cos(3x)*3)dt
СОКРАТИМ ВЫРАЖЕНИЕ НА "cos(3x)"
∫1/(5+3sin(3x))*1/9dt
УМНОЖИМ ДРОБИ:
∫1/(9(5+3sin(3x)))dt
ПОДСТАВИТЬ "5+3sin(3x)=t"
∫1/(9t)dt
ИСПОЛЬЗУЕМ СВОЙСТВО ИНТЕГРАЛОВ:
1/9*∫1/tdt
ИСПОЛЬЗУЕМ "∫1/хdx=ln(|x|)"
1/9*ln(|t|)
СДЕЛАЕМ ОБРАТНУЮ ЗАМЕНУ "t=5+3sin(3x)":
1/9*ln(|5+3sin(3x)|)+C, C∈R
ОТВЕТ: 1/9*ln(|5+3sin(3x)|)+C, C∈R