НАЙТИ НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
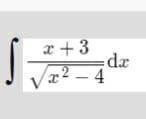
Другие вопросы по теме Алгебра
Популярные вопросы
- Узагальнення теми «Українські землі у складі Російської імперії в другій половині...
1 - Ребят, напишите красивое описание Западной Двины в виде сочинения...
2 - Почему у Гагина из произведения Ася нет имени? ...
3 - Написать сочинение-рассуждение по теме Как проявилась Душевная близость людей...
3 - Оқушы қыз бірдей бағамен тор дәптер және жолды дәптер сатып алған. Барлығы...
2 - В году весна у нас была холодной. Одна пожилая женщина, из нашего села, решила...
1 - Придумать короткий рассказ, сказку или стихотворение, в которых были бы нелепые,...
2 - 1.Бату ханның басшылығымен моңғол әскері Батыс елдеріне шабуылға шыққан жыл:...
2 - Укажите, где правда, а где ложь. Варианты ответов у прилагательных есть три...
2 - Определите разряд и степень сравнения выделенного наречия в предложении: И...
1
ответ: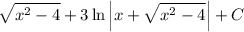
Для нахождения интеграла следует воспользоваться следующими формулами интегрирования: