Найти наименьший положительный период функции y=sinx+tgx

Как известно, если есть две периодические функции с периодами T1 и T2 , то периодом их суммы, разности и частного является число T, кратное T1 и T2.

Период sinx = 2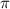k, где k - целое число.

Период tgx =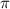 n, где n - целое число.

Наименьшим положительным периодом будет являться число 2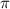, так как при k = 1 и n = 1, оно кратно обоим периодам.

Теперь проверим, что 2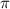 действительно является периодом функции:

f(x) = f( x + T), f( x + 2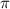) = sin(x + 2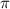) + tg(x + 2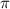) = sinx + tgx.

Как видно из вышенаписанного, число 2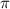 действительно является периодом функции y=sinx+tgx и является её наименьшим положительным периодом.

ответ: 2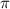

Наименьший положительный период функции - это наименьшее положительное число T, являющееся периодом данной функции.

Рассмотрим наименьшие периоды каждого слагаемого.

Для sinx  T₁=2π, для tgx T₂=π.

Период суммы - это наименьшее число, которое делится на Т₁ и Т₂.

Найти наименьший положительный период функции y=sinx+tgx   T = 2π