Найти наименьший положительный корень уравнения 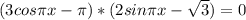
Другие вопросы по теме Алгебра
Популярные вопросы
- Сторона квадрата x см а периметр 24см с...
2 - Почему жилин и дина проявляют лучшие качества характера...
2 - Какие реки озёра города горы есть в самарской области. запишите их в сравнительной...
2 - Сколько грамм соли натрий хлор и воды необходимо чтобы приготовить раствор...
2 - Из петербурга в москву вышел товарный поезд со скоростью 48 км/ч, а через...
1 - Можно ли.назвать флягина.праведным человеком? (кратко )...
3 - Как правильно пишется пелю или пилю...
3 - Сколько граммов соли необходимо добавить к 50 грамм 8% раствора чтобы...
1 - 9,2 кг оттекті органикалық затты жаққанда, 17,2 г көмірқышқыл газы және...
1 - Напишите формулы! с ? карбонат меди 2 сульфид алюминия нитрат 2 иодид...
2
Объяснение:
и т.д.
Следовательно 1/3 - наименший положительный корень уравнения