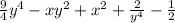 Найти наименьшее значение выражения
Найти наименьшее значение выражения
Другие вопросы по теме Алгебра
Популярные вопросы
- дам лучший ответ только все распишите. ...
1 - 10 и 11 сделайте Это по Маленькому принцу...
2 - 2. Составьте текст : «Спорт в жизни человека»...
3 - Попробуйте решить 1 и 4 задание мне нужен только ответ...
3 - В авиакомпании производится выборочное обследование трех возрастных групп пилотов...
1 - Знайдите арифматичне число...
1 - Напишите сколько получится ложноотрицательных и ложноположительных результатов...
3 - Виконайте паралельне перенесення прямокутника АВСД на вектор АС...
1 - Із Києва до Харкова одночасно виїхали автобус й автомобіль. Швидкість автомобіля...
1 - Знайдіть найбільше і найменше значення функції y=x2+16/x - 16 на проміжку (1;4)...
1
Объяснение:
Так как наименьшее значение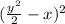 и
и 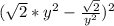 равно нулю ⇒
равно нулю ⇒
ответ: наименьшее значение выражения равно 3,5.