Найти наименьшее значение области определения √5^(2х+1)-1 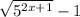
Другие вопросы по теме Алгебра
Популярные вопросы
- Подскажите, какие примеры (из жизни, из лит-ры) можно в с1 по по теме воспитание...
2 - Расставьте в клетках квадрата 6*6 различные натуральные числа так, чтобы сумма...
2 - Вкаком явление,а в ? обоснуйтеответ. а)припропускании электрического , б)принагреванииречной...
3 - При взаимодействии 9,2 г. одновалентного металла с водой выделилось 0,2 моль...
2 - Решите : в воздухе содержится 21 % кислорода по объёму. рассчитайте массу кислорода...
2 - Учеловека ген карих глаз доминирует над геном, обусловливающим голубые глаза....
3 - Сочинение на тему: 1.с чего начинается школа или 2.легко ли быть учеником?...
3 - Машина сначала проехала 30мин со скоростью 90км/ч а затем 1ч30мин со скоростью...
3 - Чем, на ваш взгляд, можно объяснить трагический для руси исход битвы на калке?...
1 - Один рабочий изготавливает 26 деталей в час,а другой -- на 3 детали больше.сколько...
3
Во-первых, выражение под корнем должно быть неотрицательным. Так как мы вычисляем корень из этого выражения, то оно должно быть больше или равно нулю. Значит, 5^(2x+1) >= 0.
Так как 5 в любой степени всегда положительное число, мы знаем, что 5^(2x+1) не может быть отрицательным. Значит, для любого значения х, значение 5^(2x+1) всегда будет положительным.
Во-вторых, у нас есть ограничение " -1", то есть после вычисления корня мы должны вычесть 1 из результата. Это ограничение следует учесть при нахождении значения х.
Теперь приступим к решению:
1. Уравнение 5^(2x+1) >= 0 не имеет ограничений на значение х, так как 5 в любой степени всегда положительное число.
2. Поскольку у нас есть вычитание 1 после вычисления корня, мы должны также проверить условие, при котором √5^(2х+1) - 1 >= 0.
3. Мы знаем, что корень из любого положительного числа всегда положителен. Значит, √5^(2х+1) всегда будет больше или равно нулю.
4. Если √5^(2х+1) - 1 >= 0, то √5^(2х+1) >= 1.
5. Наименьшее значение, при котором √5^(2х+1) >= 1, достигается при x = 0. Подставляя значение x = 0 в выражение, мы получаем: √5^(2 * 0 + 1) = √5^1 = √5 >= 1.
6. Значит, наименьшее значение области определения для данного выражения - это x >= 0.
Таким образом, ответом на вопрос является область определения √5^(2х+1) - 1: x >= 0.