Алгебра: Найти наименьшее расстояние между линиями y= x²-4x+5 и y=-4

- квадратичная функция, график - парабола, ветви которой направлены вверх. - линейная функция, график - прямая, которая параллельная оси абсцисс.Наименьшим расстоянием между данными функциями будет расстояние (перпендикуляр) от вершины параболы до прямой Координата вершины параболы: ; Так как расстояние - это перпендикуляр, то расстоянием между данными функциями будет модуль разности их ординат, так как этот перпендикуляр параллелен оси ординат, то есть единиц.ответ: 5....

Найти наименьшее расстояние между линиями y= x²-4x+5 и y=-4

Ответы

vika22888535 11.10.2020 02:04

Объяснение:

Нужно найти вершину параболы :

xвершины= -b/2a = 4/2= 2

yвершины = 4-8+5= 1

Если мы построим данный график то вершина будет в точке (2;1), а проведя второй график будет проходить через y= -4.

1+|-4|=5 - наименьшее расстояние от вершины до прямой.

ПОКАЗАТЬ ОТВЕТЫ

terckovanata 11.10.2020 02:04

$y = x^{2} - 4x + 5$ - квадратичная функция, график - парабола, ветви которой направлены вверх.

y = -4 - линейная функция, график - прямая, которая параллельная оси абсцисс.

Наименьшим расстоянием между данными функциями будет расстояние (перпендикуляр) от вершины параболы до прямой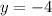 y = -4

Координата вершины параболы:

$x_{0} = \dfrac{-(-4)}{2 \cdot 1} = 2$ ;

$y_{0} = 2^{2} - 4\cdot 2 + 5 = 1$

Так как расстояние - это перпендикуляр, то расстоянием между данными функциями будет модуль разности их ординат, так как этот перпендикуляр параллелен оси ординат, то есть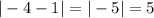 |-4 - 1| = |-5| = 5 единиц.