Найти наибольшее значение параметра 'a', при котором уравнение: x^2-5x+6+sqrt(ax-2a)*(x-3)-6ax+18a=0 имеет единственное решение.

Ответы

Gvgvv 03.07.2020 08:56

$x^2-5x+6+\sqrt{ax-2a}(x-3)-6ax+18a=0\\ (x-2)(x-3)+(x-3)\sqrt{a(x-2)}-6a(x-3)=0\\ (x-3)(x-2+\sqrt{a(x-2)}-6a)=0$

$x_1=3;~~~ a(x-2)\geq 0~~~~where~~~ a\geq0$

Если х =3 , то, подставляя в уравнение, получим a = 1/4

$x-2+\sqrt{a(x-2)}-6a=0$ - квадратное уравнение относительно $\sqrt{x-2}$

$D=(\sqrt{a})^2-4\cdot (-6a)=25a\geq 0\\ \\ \sqrt{x-2}=\dfrac{\sqrt{a}\pm5\sqrt{a}}{2}=\left[\begin{array}{ccc}-2\sqrt{a}\\ 3\sqrt{a}\end{array}\right$

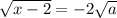Уравнение $\sqrt{x-2}=-2\sqrt{a}$ решений не имеет для $a\geq 0$

$\sqrt{x-2}=3\sqrt{a}~~~\Rightarrow~~~ x-2=9a~~~\Rightarrow~~~ x_2=9a+2$

$\displaystyle \left \{ {{a<0} \atop {9a+2\leq 2}} \right. ~~~\Rightarrow~~~~a <0$

При $a \in (-\infty ;0)\cup\{\frac{1}{4}\}$ уравнение имеет единственное решение. Наибольшее a = 1/4

ПОКАЗАТЬ ОТВЕТЫ

alexstew1 03.07.2020 08:56

Объяснение:

вынесем за скобки общие множители

x²-5x+6+[√(a(x-2))](x=3)-6a(x-3)=0 (1)

x²-5x+6 разложим на множители

х₁=-2;x=3 нашел подбором с использованием теоремы Виета

1. при а=0 выражение (1) принимает вид x²-5x+6=0 и имеет два решения

по формуле ax²+bx+c=a(x-x₁)(x-x₂)

x²-5x+6=(x+2)(x-3) подставим в (1)

(x+2)(x-3)+[√(a(x-2))](x=3)-6a(x-3)=0 вынесем за скобки общий множитель

(x-3)(x+2)+[√(a(x-2))]-6a)=0 это выражение имеет решение х=3

очевидно что, чтобы выражение (1) имело единственное решение выражение x+2+[√(a(x-2))]-6a=0 (2) не должно иметь решений

преобразуем выражение (2)

√(a(x-2))=-х+(6a-2) решим это уравнение графическим

у=√(a(x-2))

у=-х+(6a-2)

чтобы уравнение (2) не имело решений надо найти такое а при котором графики указанных выше функций не пересекались

выясним взаимное расположение графиков в зависимости от параметра а

2. При а>0

графиком у=√(a(x-2)) является кривая линия получающаяся из линии у=√х переноса вдоль оси ОХ на 2 единицы вправо и сжатием - растяжением вдоль оси ОХ в зависимости от значения а

крайняя левая по оси ОХ точка кривой (2;0) , ветка кривой направлена вправо .

так как a>0 (6a-2)>-2

2.1. при (6a-2)=2 прямая у=-х+(6a-2) имеет вид у=-х+2 и проходит через точку (2;0) и графики пересекаются в этой точке, при этом (2) имеет одно решение

2.2 при 6a-2>2 прямая у=-х+(6a-2) находится выше прямой у=-х+2 и и графики пересекаются в двух точках при этом (2) имеет 2 решения

2.3 при 6a-2<2 прямая у=-х+(6a-2) находится ниже прямой у=-х+2 и и графики не пересекаются (2) не имеет решений

при этом

6a-2<2 ; 6a<4; a<4/6; a<2/3 с учетом того что мы рассматриваем a>0

0<a<2/3

3. При а<0

крайняя правая относительно оси ОХ точка кривой (2;0) , ветка кривой направлена влево .

так как a<0 то (6a-2)<-2

так как (6a-2)<-2

прямая у=-х+(6a-2) в этом случае находится ниже прямой у=-х-2

которая имеет с графиком кривой общую точку и тоже имеет с графиком кривой общую точку

в этом случае (2) имеет решение