1. Алгебра
  2. Найти наибольшее отрицательное

Найти наибольшее отрицательное решение в градусах

coolplayer1 coolplayer1    2   16.07.2022 01:03    0

Ответы
movsisjan88 movsisjan88  16.07.2022 01:04

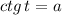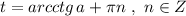Решение уравнения  ctg\, t=a  имеет вид   t=arcctg\, a+\pi n\ ,\ n\in Z  .

ctg(4x-\dfrac{\pi}{3})=-\sqrt34x-\dfrac{\pi}{3}=arcctg(-\sqrt3)+\pi n\ \ ,\ n\in Z4x-\dfrac{\pi}{3}=-\dfrac{\pi}{6}+\pi n\ \ ,\ n\in Z4x=\dfrac{\pi}{3}-\dfrac{\pi}{6}+\pi n\ \ ,\ n\in Z4x=\dfrac{\pi}{6}+\pi n\ \ ,\ n\in Zboxed{\ x=\dfrac{\pi}{24}+\dfrac{\pi n}{4}\ \ ,\ n\in Z\ }    

Отрицательные решения :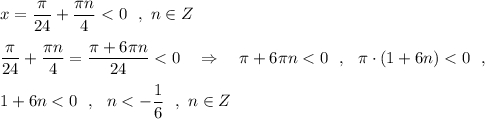    x=\dfrac{\pi}{24}+\dfrac{\pi n}{4} < 0\ \ ,\ n\in Zdfrac{\pi}{24}+\dfrac{\pi n}{4}=\dfrac{\pi +6\pi n}{24} < 0\ \ \ \Rightarrow \ \ \ \pi +6\pi n < 0\ \ ,\ \ \pi \cdot (1+6n) < 0\ \ ,1+6n < 0\ \ ,\ \ n < -\dfrac{1}{6}\ \ ,\ n\in Z

Отрицательные решения будем получать при целых  n  , которые меньше  -1/6 , то есть при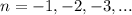  n=-1,-2,-3,...   А наибольшее отрицательное решение получим при  n=-1 :

\boldsymbol{x}=\dfrac{\pi}{24}+\dfrac{\pi \cdot (-1)}{4}=\dfrac{\pi -6\pi }{24}=\boldsymbol{-\dfrac{5\pi }{24}=-37,5^\circ }      - ответ  

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Яринка05 Яринка05  09.09.2019 14:00
Спортивный магазин проводит акцию. любой свитер стоит 800 руб. при покупке двух твиттеров – скидка на второй свитер 70%.сколько рублей придётся заплатить за покупку...
Kotliarrostislav Kotliarrostislav  09.09.2019 14:00
Последовательность (a_{n}) задана формулой a_{n}= \frac{34}{n+1}. сколько членов этой последовательности больше 6? ответ дать более развернутый....
makuxina makuxina  09.09.2019 14:00
Представьте в виде степени выражение -m^7...
nickartyar nickartyar  09.09.2019 14:00
Вероятность того, что новое шариковая ручка пишет плохо (или не пишет ), равна 0,12. покупатель в магазине выбирает одну шариковую ручку. найдите вероятность того...
кріс2 кріс2  09.09.2019 14:00
Сколько точек пересечения в зависимости от параметра а имеют графики функций у=ах-2 у=2х+а...
1innic11 1innic11  22.12.2020 16:12
Математика уравнение линейные ДУ Нужно решение уравнения, заранее Задание:Тема занятия « ЛИНЕЙНЫЕ ДУ». Их решают двумя методами. Чаще используют первый метод-МЕТОД...
lanceva3 lanceva3  22.12.2020 16:11
Нужно решение задачи. Через точки A(-5;1) и B(-1;-2) проходит прямая L1. Найдите уравнение прямой L2, которая перпендикулярна L1 и проходит через точку C(3;-3). После...
1amon1 1amon1  22.12.2020 16:10
1.Из формулы y=ab/2c вырази c и найди значение, если a=26,b=4,02,y=4 Варианты ответов:1.c=ab/2y 2. C=2aby 3.c=2y/abФормула:ответ: (запиши без округления) 2. Вырази...
Ryuuko Ryuuko  16.12.2019 09:36
Y=-2sin(x/2+п/6)-2 построить график....
DARINASTAR98 DARINASTAR98  16.12.2019 09:36
Найдите область определения функции f(x)=x-4/x2-x-6​...

Популярные вопросы