Найти наибольшее и наименьшее значение выражения 4cosα+3sinα
Ответы
Можно так
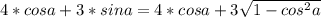 , по неравенству Коши - Буняковского
, по неравенству Коши - Буняковского
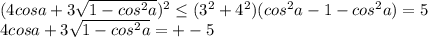
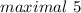
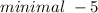
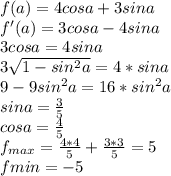
ПОКАЗАТЬ ОТВЕТЫ
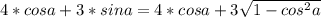 , по неравенству Коши - Буняковского
, по неравенству Коши - Буняковского 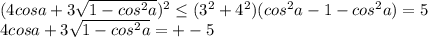
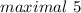
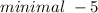
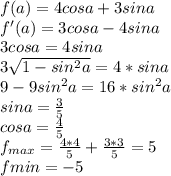
Другие вопросы по теме Алгебра
Популярные вопросы
- Линии тропиков и полярных кругов являются 1.климатических поясов...
2 - Исправьте речевые ошибки.запишите предложения исправленном виде....
1 - Составте словосочмтание its a sunny morning dosent he kate is lying...
2 - Даны векторы а{2; 4}и b{-3; 2} найдите кординаты...
1 - Решите уравнение. ! одна пятая икс равно минус пять...
1 - Найди неизвестный делимые в равенства x÷4=9 (ост 2)...
2 - Дано трикутник зі сторонами 13,20,21 а)доведіть що даний трикутник...
3 - Двигается 36 км/ч за 30 минут какой путь?...
3 - Два поезда одновременно вышли навстречу друг другу со станций расстояние...
3 - Распределить слова в две группы по частям речи.обозначьте суффиксы:...
1