Найти наибольшее и наименьшее значение функции(с полным решением: 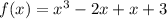
На отрезке: [0, 3/2]
![Найти наибольшее и наименьшее значение функции(с полным решением: На отрезке: [0, 3/2]](/tpl/images/4772/1438/c32dc.jpg)
Другие вопросы по теме Алгебра
Популярные вопросы
- 2. Запропонуй ситуацію, вирішення якої вимагає використання знань право...
3 - решить эти два уравнения, буду очень благодарна нужно...
2 - Литература влияет на музыку, а музыка на литературу нет. Музыка и литература...
1 - 5 1/7-( 5,7 : 3 + 1 7/9) =...
2 - Опишите морфологическое строение хромосом и назовите их типы...
3 - Английские пословицы которые похоже на русские зонт готов при ясной погоде...
3 - Определите диаметр каждого из шаров. Коков радиус каждого шара? ...
1 - Почему М.Ауезова называли великим писателем?...
1 - Приведите 3 примера товаров из других стран...
1 - нужно написать битву при Платье история 6 класс...
2
f(x) = x³ - 2x + x + 3
⠀⠀= x³ - x + 3
Находим производную
f'(x) = 3x² - 1
Находим экстремумы
3x² - 1 = 0
3x² = 1
x² = 1/3
x = ± √(1/3)
Освобождаемся от иррациональности в знаменателе
x₁ = - √3 / 3 (≈ -0,6)
x₂ = √3 / 3 (≈ 0,6)
Только второй корень входит в заданный интервал [0 ; 3/2], находим значение функции для него
f(√3 / 3) = (√3 /3)³ - (√3 /3) + 3 = -(2√3 - 27) / 9 (≈ 2,6)
Найдём значения функции при x = 0 и x = 3/2 (границы интервала)
f(0) = 0³ - 0 + 3 = 3
f(3/2) = (3/2)³ - (3/2) + 3 = 39/8 (≈ 4,9)
ответ
- Наименьшее значение функции равно -(2√3 - 27) / 9, и достигается оно при x = √3 / 3.
- Наибольшее значение функции равно 39/8, и достигается оно при x = 3/2.