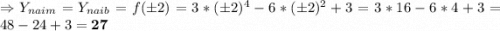Найти наибольшее и наименьшее значение функции на отрезке
f(x)3x^4-6x^2+3 на отрезке [-2;2]
Другие вопросы по теме Алгебра
Популярные вопросы
- Назовите металлы, которые плавают в ртути....
2 - Скакую форму имеют магнитные линии прямого проводника с током?...
2 - Сколько существует выбрать набор из k элементов, если первый...
3 - 1) составьте где это требуется молекулярные и ионные уравнения...
2 - С. 1)после погружения цинковой пластинки массой 100 г в раствор...
3 - Напишите рассуждение.вот вопросы: нужно ли мстить за причинённую...
2 - Представьте многочлен в виде квадрата двучлена...
3 - Постройте график функции (0,25x^2+0,5x)|x|y= x+2распишите ...
3 - Замени t одночленом так, чтобы получился квадрат двучлена t^2+5x+16x^2...
3 - Запишите факты о битве о фермопил(явление , менее двух фактов)...
1
Объяснение:
область определения функции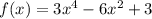 - симметричное множество
- симметричное множество 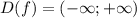 .
. 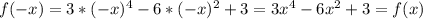 , значит, функция четная,
, значит, функция четная,